极限与连续导数与微分的概念

Table of contents

一、极限

极限可以称得上一个理想概念，即无限接近而不到达。极限又分函数极限和数列极限，前者为微积分基础，后者为级数的先导。

一个函数在某一点的极限存在，指自变量无限接近该点时，因变量则无限接近该极限值。

1.1 数列的极限

定义：

设{$X_n$}为一数列，如果存在常数$a$ ,对于任意给定的正数$\epsilon$(无论她多么小)，总存在正整数 $N$，使得当$n>N$时，不等式 $x_n-a |< \epsilon$ 都成立，那么就称$a$是数列{$X_n$}的极限，或者称数列{$x_n$}收敛于$a$，记为

或 $x_n \to a(n \to \infty)$

收敛数列的性质：

定理1（极限的唯一性） 如果数列{$X_n$}收敛，那么它的极限唯一.

定理2（收敛数列的有界性） 如果数列{$X_n$}收敛，那么数列{$X_n$}一定有界.

定理3（收敛数列的保号性） 如果 $\textcolor{red}{\lim\limits_{n\to\infty} x_n = a}$ 且 $a>0$(或$a<0$)，那么存在正整数$N$，当$n>N$时，都有$x_n>0$(或$x_n<0$)

推论 如果数列{$X_n$}从某项起有$X_{n} \geq 0$或$X_n\leq0$，且$\textcolor{red}{\lim\limits_{n\to\infty} x_n = a}$ 那么$a\geq0$(或$a\leq0$)

定理4（收敛数列与其子数列间的关系） 如果数列{$X_n$}收敛于$a$，那么它的任意子数列也收敛，且极限也是$a$

1.2 函数的极限

定义1：

设函数$f(x)$，在点$x_0$的某一去心邻域有定义

如果存在常数 $A$，对于任意给定的正数$\epsilon$（无论它多么小），总存在正数 ，使得当x满足不等式 $0 < |x_n - x_0| < \delta$时，对应的函数$f(x)$都满足不等式

那么常数A就叫做函数 $f(x)$在$x \to x_0$的极限， 记作

或$f(x) \to A$当($x \to x_0$)

简述为：

定义2：

设函数$f(x)$当$|x|$大于某一正数时有定义.如果存在常数$A$，对于任意给定的正数$\epsilon$ (无论它多么小），总存在正数$X$，使得当$|x|>X$时，对应的函数$f(x)$都满足不等式

那么常数A就叫做函数 $f(x)$在$x \to x_0$的极限， 记作

或$f(x) \to A$当($x \to x_0$) 简述为：

函数极限的性质

定理1（函数极限的唯一性）：如果

存在，那么极限唯一。

定理2（函数极限的局部有界性）：如果

那么存在常数$M>0$和$\delta>0$,使得当$0 < |x - x_0| < \delta$时有$|f(x)| \leq M$

定理3（函数极限的局部保号性）：如果

且$A>0$(或$A<0$), 那么存在常数$\delta>0$,使得当$0 < |x - x_0| < \delta$时有$f(x)>0$或($f(x)<0$)

定理3：如果$\lim\limits_{x \to x_{0}} f(x) = A (A \neq 0)$那么就存在$x_0$的某个去心邻域$U(x_0)$,

当$x \in \dot{U}(x_0)$,就有$|f(x)| > \frac{|A|}{2}$

推论 如果在$x_0$的某个去心邻域$f(x) \geq 0$(或$f(x) \leq 0$)而且$\lim\limits_{x \to x_0} f(x) = A$,

那么$A \geq 0$(或$A \leq 0$)

定理4（函数极限与数列极限的关系）：如果极限$\lim\limits_{x \to x_0} f(x)$

存在{$X_n$}为函数$f(x)$的定义域内任一收敛于$x_0$的数列,且满足$x_{n} \neq x_{0}(n \in N^{+})$,那么相应的函数值数列{$f(x_n)$}必收敛，且$\lim_{n\to\infty} f(x_n) = \lim_{x\to x_0} f(x)$

无穷大与无穷小

定理1：在自变量的同一变化过程$x \to x_0$(或$x \to \infty$)中，函数$f(x)$具有极限A的充要条件是$f(x) = A + a$,其中$a$为无穷小

极限存在准则 、两个重要极限

准则1： 如果数列{$x_n$},{$y_n$},{$z_n$}满足下列条件：

（1）从某项起，即$\exists n_0 \in {N}_+$当$n>n_0$时，有

（2）

那么数列{$x_n$}的极限存在，且

推广：如果

（1）当$x\in \mathring{U}(x_0,r) \ (\text{或} |x|>M) \text{时}, g(x) \leq f(x) \leq h(x)$

（2）$\lim g(x) = a, \lim h(x) = a$ 那么

准则 2： 单调有界数列必有极限.

推论 ： 设函数$f(x)$在点$x_0$的某个左领域内单调并且有界，则$f(x)$在$x_0$的左极限$f(x_{0}^{-})$必定存在

柯西极限存在准则

数列{$X_{n}$}收敛的充分必要条件是：

对于任意给定的整数$\epsilon$，存在正整数$N$,使得当$m>N, n>N$ 时，有

函数的连续性与间断点

连续性:

定义：设函数$y = f(x)$在点$x_{0}$的某一领域内有定义，如果

那么就称函数$y = f(x)$在点$x_{0}$连续。

或：设函数$y = f(x)$在点$x_{0}$的某一领域内有定义，如果

那么就称函数$y = f(x)$在点$x_{0}$连续。

简述为:

左连续：

如果

存在且等于$f(x_0^-)$ ，即

那么就说$f(x)$在点$x_{0}$左连续。

右连续：

如果

存在且等于 $f(x_{0}^{+})$ ，即

那么就说$f(x)$在点$x_{0}$右连续。

间断点： 第一类间断点：

若$x_0$为间断点，$f(x_{0}^{-})$和$f(x_{0}^{+})$的极限都存在，则为第一类间断点.

第二类间断点：

不是第一类的任何间断点，称为第二类间断点.

*在第一类间断点中，左右极限相等者称为可去间断点，不相等者称为跳跃间断点.无穷间断点和震荡间断点显然属于第二类间断点.

二、连续

三、导数

定义：

设函数 $y = f(x)$ 在点 $x_0$ 的某邻域内有定义，当自变量$x$在 $x_0$ 处取得增量$\Delta x$（点仍在该邻域内）时，相应的函数值取得增量 $\Delta y = f(x_0 + \Delta x) - f(x_0)$ ；如果当 $\Delta x \to 0$  时，$\Delta y$ 与 $\Delta x$ 之比的极限存在，则称函数在$x_0$ 处可导，并称这个差商的极限为函数$y = f(x)$在点 $x_0$处的导数，记为 $f'(x_0)$ ，即

注：

1. 函数 $f(x)$在点 $x_{}0$ 处可导有时也可说成 $f(x)$ 在点 $x_{}0$ 处具有导数或导数存在。

2. 关于 (1) 式还有另外一种写法：$\textcolor{red}{f'(x_0)= \lim\limits_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}}$

3. 关于 (2),(3),(4) 式，是导数三种不同的记号，表示在 $x=x_{}0$ 处的导数，即

4. 函数增量 $\Delta y$ 与自变量增量 $\Delta x$ 的比值是函数值从 $x_0$ 到 $x_0+\Delta x$ 区间上的平均变化率，而$y'(x_0)$ 或 $\frac{dy}{dx}\Big|_{x=x_0}$ 或 $\frac{df(x)}{dx}\Big|_{x=x_0}$ 是函数在 $x_0$ 点的变化量，它反映的是函数值随自变量的变化快慢程度。

5. 如果 $\lim\limits_{\Delta x\to 0}\frac{\Delta y}{\Delta x}=\infty$，这时$y=f(x)$ 在 $x_0$ 处不可导，但是有时候也说 $y=f(x)$ 在 $x_0$ 处的导数是无穷大，此时曲线$y=f(x)$ 在 $x_0$ 处的曲线垂直于 $x$ 轴，如下图：

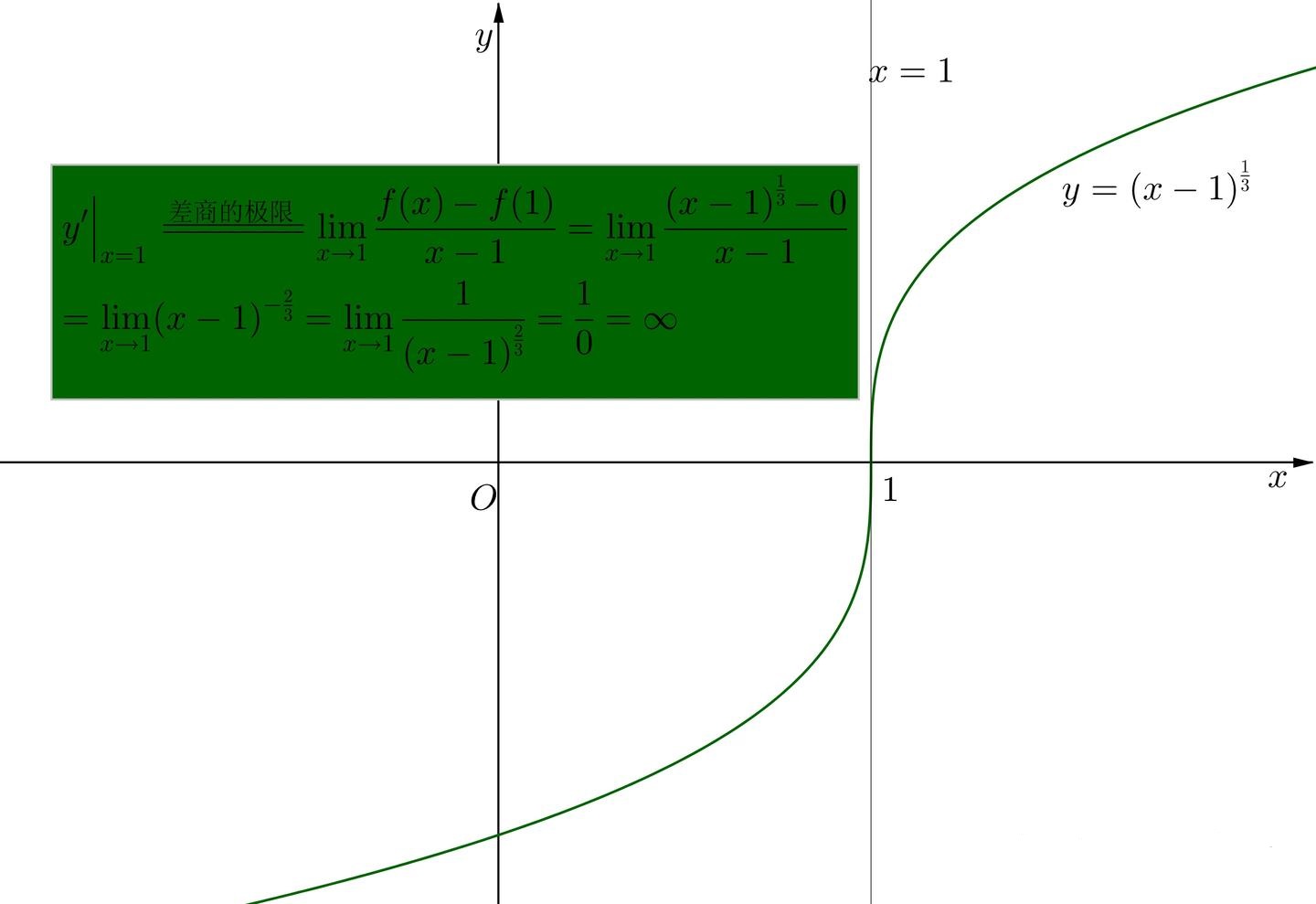
6. 如果$f(x)$ 在开区间 $I$ 内的每一点都可导，则称 $f(x)$ 于区间 $I$ 可导，这时对应于区间 $I$ 内的每一点 $x$ 都有一个确定的导数值，这样就得到了一个新的函数，它称为原函数 $f(x)$ 的导函数，记作 $y'(x)$ 或 $\frac{\mathrm d y}{\mathrm dx}$ 或 $f'(x)$ ，即：$f'(x)=\frac{\mathrm d y}{\mathrm dx}=\lim\limits_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$ ，显然 $f'(x_0)$ 是导函数 $f'(x)$ 在 $x_0$ 点处的函数值。导函数 $f'(x)$ 与 $f'(x_0)$ 在不引起混乱的情况下都称为导数。

四、微分

五、积分